Ada berapa lampu yang tidak bisa dinyala/matikan karena tak terhubung dengan saklar?
A. 0
B. 1
C. 5
D. 6
E. 25

Sugeng ingin agar rumahnya terang benderang, karena dia takut akan kegelapan. Ada berapa lampu maksimal yang bisa menyala secara bersamaan?
A. 5
B. 13
C. 15
D. 16
E. 24

Berapa banyak cara memasang domino 1x2 agar menutupi seluruh papan berukuran 3x4? Domino tidak dapat dipotong, maupun bertumpukan dengan domino lain. Selain itu seluruh bagian domino harus berada di dalam papan. Setiap domino dapat diputar/dirotasi.
A. 3
B. 11
C. 9
D. 10
E. 18

Ada seekor katak yang ingin menyeberangi suatu sungai. Di sungai tersebut, terdapat dua jenis benda sungai, yaitu batu yang dapat ditempati katak, dan daun yang tidak dapat ditempati katak. Seekor katak dapat melompat ke benda tepat di depannya atau dapat melompatinya (dengan kata lain, menempati bendakedua yang ada di depannya). Berapa banyak cara yang bisa ditempuh katak untuk menyeberangi sungai dengan selamat (dengan tidak menginjak daun) jika konfigurasi benda di sungai adalah sebagai berikut (katak menyeberang dari kiri ke kanan)

A. 1
B. 3
C. 2
D. 6
E. 10

Pak Zaki memiliki 12 buah permen yang akan dibagikan kepada 3 orang cucunya, yaitu Abi, Bibi, dan Cibi. Permen yang dibagikan tidak bersisa. Dalam pembagian tersebut bisa saja ada cucu yang tidak mendapatkan permen sama sekali. Tentu saja, satu permen tidak bisa dibagi kepada lebih dari satu orang. Karena Cibi merupakan cucu kesayangan Pak Zaki, maka Cibi selalu mendapat lebih dari 6 permen. Berapakah banyak cara Pak Zaki membagikan permen tersebut ke cucu-cucunya? Suatu cara dianggap berbeda jika banyak permen yang diterima salah satu orang berbeda
A. 20
B. 364
C. 60
D. 128
E. 21

Sebuah toko menjual donat dengan rasa yang berbedabeda. Terdapat 4 jenis rasa donat yang dijual, yaitu Stroberi, Coklat, Vanilla, dan Cappucino. Pak Dengklek ingin membeli 4
buah donat. Berapa banyak kemungkinan Pak Dengklek untuk membeli donat-donat tersebut?
A. 9
B. 24
C. 256
D. 1
E. 35

Pada sebuah pesta pernikahan terdapat 100 pasangan suami istri. Setiap suami tidak akan bersalaman dengan istrinya sendiri. Berapa jumlah salaman yang terjadi dalam pesta itu?
A. 20100
B. 19110
C. 19800
D. 20503
E. 20301

Di suatu pulau misterius terdapat 2 macam orang, prajurit dan pencuri. Sang prajurit selalu berkata jujur dan sang pencuri selalu berkata bohong. Suatu hari Anda bertemu tiga orang yang berkata seperti berikut:
A: Hanya satu diantara kami yang merupakan prajurit
B: Setidaknya satu dari antara kita adalah prajurit
C: A bukanlah prajurit
Siapakah diantara mereka yang merupakan prajurit?
A. Hanya A
B. Hanya B
C. Hanya C
D. B dan C saja
E. A dan B saja

Suatu negara dengan 3 kota, ditunjukkan dalam diagram berikut.

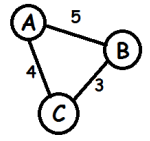
Berapakah panjang rata­-rata rute perjalanan dari seluruh permutasi?
A. 8.0
B. 8.5 
C. 9.0
D. 9.5
E. A, B, C, D salah atau ada lebih dari satu jawaban yang benar di antara A, B, C, D

Untuk menuliskan N bilangan asli pertama secara berderet dibutuhkan 2013 digit, berapakah nilai N yang memenuhi? {catatan: bilangan asli adalah 1, 2, 3, ...}  
A. 706
B. 707
C. 708
D. 709
E. 710

Berapa banyak persegi panjang yang dapat terbentuk dalam papan catur berukuran n*n?
A. n^2  {catatan: n^2 berarti n pangkat 2}
B. (n(n+1)/2)^2
C. n(n+1)(2n+1)/6
D. n(n+1)(3(n^2)+n­1)/6
E. (3n+1)*(n+2)!/4!*(n­1)!

Ada berapa buah bilangan dari 1 sampai 10000 (inklusif) yang memiliki minimal 1 buah digit ‘1’?
A. 3250
B. 3430
C. 3440
D. 3456
E. 3630

Dua orang dewa, Dewa Warisan dan Dewa Sembilanbelas masing­masing memiliki 5 orang anak. Semua anak Dewa Warisan berjenis kelamin laki­-laki, sedangkan semua anak dari Dewa Sembilanbelas berjenis kelamin perempuan. Rencananya, mereka akan saling menjodohkan kelima anak mereka. Setiap anak mempunyai nilai. Nilai dari anak­-anak Dewa Warisan adalah {2,­3,5,9,­6,}. Sedangkan nilai dari anak­-anak Dewa Sembilanbelas adalah {7,0,­4,8,­1}. Dari sebuah pernikahan anak mereka, mereka akan mendapatkan tambahan kebahagiaan yang direpresentasikan dalam bentuk bilangan. Didefinisikan, jika mereka menikahkan anak bernilai A dengan anak bernilai B, mereka akan mendapatkan kebahagiaan sebesar AxB. Berapa total kebahagiaan maksimal yang bisa mereka peroleh?
A. 134
B. 143
C. 108
D. 104
E. 165

Berapakah n minimal sedemikian sehingga n! memiliki 2013 angka nol dibelakangnya? ( n! = nx(n­1)x...3x2x1 )  {catatan: n! berarti n faktorial}
A. 8065
B. 8064
C. 8060
D. 8051
E. 8050

Apabila nilai N = 5 dan langkah tersebut dilakukan sebanyak 45 kali kartu apa yang terdapat pada tumpukan teratas?
A. 24
B. 25
C. 26
D. 27
E. 28

Jika N = 7 dan langkah tersebut dilakukan sebanyak 50 kali, kartu apa yang terdapat pada tumpukan teratas?
A. 22
B. 23
C. 24
D. 25
E. 26

Apabila nilai N = 3 berapa kali anda harus melakukan langkah tersebut agar kartu yang bernilai 2 terdapat pada tumpukan teratas?
A. 7
B. 8
C. 9
D. 10
E. 11

Berapa langkah minimal yang dibutuhkan untuk mengurutkan deret {3, 2, 1, 5, 7, 4, 8, 6, 10, 9} secara menaik apabila langkah yang hanya dapat anda lakukan adalah menukar posisi dari 2 buah bilangan manapun?
A. 4
B. 5
C. 6  
D. 7
E. 8

Berapa segitiga paling banyak yang dapat dibentuk dengan menggambar tiga segitiga yang saling bertindihan?
A. 15
B. 24
C. 27
D. 30
E. Lebih dari 30

Ada pipa air horizontal berbentuk lingkaran yang terisi sebagian. Jika dilihat secara melintang, ketinggian air adalah 24 cm, sedangkan lebar air pada permukaannya juga 24 cm. Berapakah diameter pipa tersebut?

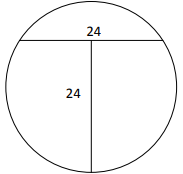
A. 28 cm
B. 30 cm
C. 32 cm
D. 36 cm
E. Jawaban A, B, C, D salah

Di dalam sebuah industri Air Minum, terdapat sistem pipa seperti yang ditunjukkan oleh gambar berikut ini.

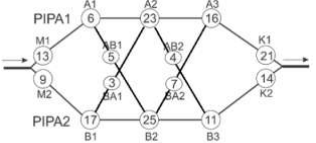
Air akan bergerak dari kiri ke kanan. Setiap lingkaran menunjukkan keran­keran yang dapat dibuka untuk mengalirkan air. Pada awalnya seluruh keran dalam keadaan tertutup. Biaya yang dibutuhkan untuk membuka suatu keran dinyatakan dengan angka yang tertulis di atas keran tersebut. Industri tersebut akan membuka beberapa keran agar air dapat mengalir tanpa hambatan. Sebagai contoh, dapat dibuka keran M1, A1, A2, A3, dan K1 sehingga air dapat mengalir; total biaya yang dibutuhkan adalah 13 + 6 + 23 + 16 + 21 = 79. Industri tersebut tentu saja tidak akan membuka semua kran yang ada. Biaya minimum yang dapat dikeluarkan industri tersebut untuk mengalirkan air dari kiri ke kanan adalah
A. 69
B. 71
C. 75
D. 79
E. 81

Kartu bridge berjumlah 52 buah kartu yang terdiri dari 4 macam daun dan 13 nilai. Daun tersebut meliputi sekop, keriting, hati, dan diamond, sedangkan nilainya meliputi 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, dan A. Dalam permainan five­card draw, setiap orang mendapatkan 5 buah kartu. Terdapat istilah Four of Kind, yaitu kondisi dimana seseorang memiliki 4 buah kartu yang dengan nilai yang sama. Banyaknya kemungkinan terjadinya Four of Kind adalah ...
A. 613
B. 615
C. 620
D. 624
E. 631

Terdapat istilah Full House yaitu kondisi dimana seseorang memiliki 3 kartu dengan nilai X dan 2  kartu dengan nilai Y, di mana X tidak sama dengan Y. Banyaknya kemungkinan terjadinya Full House adalah ...
A. 144
B. 2048
C. 2144
D. 3096
E. 3744

Pada perlombaan reli jarak jauh, terdapat 5 peserta dengan karakteristik sebagai berikut 

Andy: kecepatan berkendara  100 km/jam, setiap 80 km, akan berhenti cek mesin selama 45 menit
Budi:  kecepatan berkendara 80 km/jam, setiap 75 km, akan berhenti cek mesin selama 30 menit
Cory:  kecepatan berkendara 100 km/jam, setiap 70 km, akan berhenti cek mesin selama 15 menit
Didy:  kecepatan berkendara 80 km/jam, setiap 65 km, akan berhenti cek mesin selama 12 menit
Erna:  kecepatan berkendara 100 km/jam, setiap 60 km, akan berhenti cek mesin selama 6 menit

Siapakah pemenang perlombaan internasional ini apabila jarak tempuh dari garis start hingga finish adalah 1000 km?
A. Andy
B. Budi
C. Cory
D. Didy
E. Erna

Dari deskripsi soal di atas, jika E sedang ingin tidur, sehingga dia duduk di sebelah jendala pada barisan paling belakang, maka ada berapa kemungkinan posisi duduk yang dapat dibentuk?
A. 4
B. 5
C. 6
D. 7
E. 8

Dari deskripsi soal di atas, jika E sedang ingin tidur, sehingga dia duduk di sebelah jendela pada barisan paling belakang, dan G tidak duduk di barisan paling depan,maka dapat kita pastikan, bahwa orang yang duduk di posisi 1 adalah..
A. A
B. B
C. C
D. D
E. E

Berapa banyak untaian bit dengan panjang 10 yang diawali 000 atau diakhiri 1111?  
A. 192
B. 184
C. 176
D. 128
E. Pilihan A, B, C, dan D salah.

Asosiasi TOKI merupakan organisasi yang anggotanya alumni TOKI. Seseorang dapat disebut alumni TOKI jika sudah tidak memenuhi syarat mengikuti IOI dan pernah mengikuti pelatnas. Seseorang dapat mengikuti pelatnas bila pernah mendapatkan medali saat OSN. Jika seseorang telah berusia lebih dari 21 tahun atau telah memasuki perguruan tinggi, maka dia tidak memenuhi syarat mengikuti IOI. Seseorang yang akan mengikuti IOI harus mengikuti pelatnas. Cakra saat ini adalah mahasiswa dari universitas XX dan mendapat pernah medali Emas OSN, Basith adalah mahasiswa dari universitas YYY dan pernah mengikuti pelatnas, sedangkan Nathan adalah siswa SMA Z yang pernah dapat medali perak IOI.
Pernyataan:
I. Basith adalah anggota asosiasi alumni TOKI.
II. Cakra adalah alumni TOKI.
III. Nathan pernah mengikuti pelatnas.
IV. Cakra pernah mengikuti IOI.
Dari pernyataan­-pernyataan di atas, manakah yang pasti benar?
A. I, IV
B. II, IV
C. II, III
D. I, III
E. I, II, III

Terdapat sebuah nomor telepon abc­defg. Sebuah nomor telepon yang mudah diingat adalah sebuah nomor yang memenuhi (abc=def) atau (abc = efg) (di sini, abc menyatakan bilangan tiga digit abc). Ada berapa kemungkinan nomor telepon yang mudah diingat?
A. 9000
B. 9990
C. 14985
D. 19980
E. 19990

Dari bilangan bulat 1 hingga 2013, berapakah jumlah bilangan yang habis dibagi 3, 5 atau 7 tetapi tidak habis dibagi 21 dan 35?
A. 943
B. 960
C. 971
D. 1067
E. 1093

function panggil1(x:longint):longint;
begin
  if (x<3) then panggil1:=0
  else panggil1:=panggil1(x-1)+2*panggil1(x-2)+3;
end; 

Bila fungsi di atas dipanggil dengan panggil1(7), maka hasil keluarannya adalah:
A. 7
B. 28
C. 34
D. 63
E. 97

function sikat(x,y:longint):longint;
begin
  if (x>=y) then sikat:=x
  else sikat:=3*sikat(x+1,y)+2*sikat(x,y-1);
end; 

Bila fungsi di atas dipanggil dengan sikat(1,3), maka hasi keluarannya adalah:
A. 18
B. 55
C. 89
D. 103
E. 237

function hitung(n:integer):integer;
begin
  if(n=0)then hitung:=0
  else hitung:=hitung(n div 5) + (n mod 5);
end;

Berapa nilai dari hitung(2903)?
A. 14
B. 10
C. 11
D. 13
E. 12

function wow(n:integer):integer;
var
  res, i, cnt : integer;
begin
  res:=1;
  for i:=2 to n do
    if(n mod i = 0) then begin
      cnt:= 0;
      while (n mod i = 0) do
      begin
        n:=n div i;
        cnt:= cnt+1;
      end;
      res:=res*(cnt+1);
    end;
  wow:=res;
end; 

Berapakah n mininum sehingga wow(n) bernilai 10?
A. 32
B. 512
C. 1000
D. 48
E. 38

var
  head, tail, x : integer;
  stek: array [1..100] of integer;
function pop():integer;
begin
  if (head = tail) then
    pop := -1
  else
  begin
    pop := stek[head];
    head := head + 1;
  end;
end;

begin
  stek[3] := 5;
  stek[2] := 3;
  stek[4] := 7;
  stek[1] := 1;
  stek[5] := 9;
  head := 1;
  tail := 6;
  pop();
  for x := 1 to 3 do writeln( pop() );
  pop();
end.

Jika program tersebut dijalankan, maka pada layar akan tampil:
A. 3
    7
    1
    
B. 5
    3
    7
    1
    9
    
C. 3
    5
    7
    
D. 1
    3
    5
    7
    9
    
E. ­1

Diberikan potongan program berikut:

pop();
for x := 1 to 3 do writeln( pop() );
pop(); 

jika potongan program tersebut diganti dengan

for x := 1 to 3 do
  if (pop() <> -1) then writeln( pop() ); 

berapakah outputnya sekarang?
A. 3
    7
    1
    
B. 3
    1
    ­1
    
C. 3
    5
    7
    
D. 3
    7
    ­1
    
E. ­1
    ­1
    ­1

Berapakah hasil dari Bunga(3)?
A. 1
B. 2
C. 3
D. 4
E. A, B, C, D salah atau ada lebih dari satu jawaban yang benar di antara A, B, C, D

Berapakah hasil dari Bunga(21)?
A. 2097152
B. 1048576
C. 384759
D. 404
E. A, B, C, D salah atau ada lebih dari satu jawaban yang benar di antara A, B, C, D

Apabila program di atas diberi masukan 16 8, berapakah output yang dihasilkan oleh program di atas?
A. 2
B. 24
C. 8
D. 16
E. 8

Apabila nilai x = 120 dan nilai y = 30 berapakah output yang dihasilkan oleh program di atas?
A. 40
B. 150
C. 90
D. 120
E. 30

Apabila kita perhatikan potongan program di atas adalah potongan program?
A. Menjumlahkan 2 buah bilangan bulat positif
B. Mengalikan 2 buah bilangan bulat positif
C. Mengurangi 2 buah bilangan bulat positif
D. Mencari nilai terkecil dari 2 buah bilangan bulat positif
E. Mencari nilai terbesar dari 2 buah bilangan bulat positif

const
  M=100;
var
  x,i,n,h:longint;
  A:array[1..M] of boolean;
  B:array[1..M] of longint;
begin
  for i:=1 to M do
    A[i]:=true;
  n:=0;
  for i:=2 to M do
  begin
    if A[i] then
    begin
      n:=n+1;
      B[n]:=i;
      h:=i;
      while h<M do
      begin
        h:=h+i;
        if h<=M then A[h]:=false;
      end;
    end;
  end;
  readln(x);
  writeln(B[x]);
end. 

Berapakah hasil program di atas apabila x = 10?
A. 13
B. 17
C. 20
D. 29
E. Runtime Error

var
  A: array[1..5] of longint = (1, 2, 3, 4, 5);
  i, j, t: longint;
begin
  for i := 1 to 5 do
    for j := 1 to i do begin
      t := A[i] xor A[j];
      A[i] := t xor A[i];
      A[j] := t xor A[i]
    end;
  for i := 1 to 5 do begin
    if (i <> 1) then write(' ');
    write(A[i])
  end;
  writeln;
end. 

Apa hasil dari program tersebut?
A. 2 5 4 3 1
B. 5 4 3 2 1
C. 3 1 4 2 5
D. 2 1 3 5 4
E. 1 4 2 5 3

Output yang dihasilkan jika dilakukan pemanggilan kambing(1) adalah ....
A. 3  
B. 3 9 2 6 1 4 7 8 5 10
C. 3 9 6 8 5 10 1 2 4 7
D. 8 6 5 9 10 1 3 4 2 7
E. 8 5 6 10 1 9 4 7 2 3

Agar output yang dihasilkan terurut menaik setelah pemanggilan kambing(1), maka array data harus berisi ....
A. (7,4,9,2,6,8,10,1,3,5)
B. (1,2,3,4,5,6,7,8,9,10)
C. (8,4,9,2,10,5,1,6,3,7)
D. (1,3,2,5,6,4,8,10,9,7)
E. (7,4,2,1,3,6,5,9,8,10)

i := 0;
while (x>1) do
begin
  if (x mod 2 = 1) then
    x := 3*x+1
  else
    x := x div 2;
  inc(i);
end;
writeln(i); 

Jika x = 13, maka output dari program di atas adalah ....
A. 5
B. 6
C. 7
D. 8
E. 9

Berapakah hasil dari pemanggilan fungsi def(7,100) ?
A. 1
B. 7
C. 43
D. 49
E. Jawaban A, B, C, D salah

Apabila bagian (a) diubah menjadi abc := a*2 ­ (a mod 5), maka berapakah hasil pemanggilan fungsi def(7,151)?
A. 1
B. 7
C. 43
D. 49
E. Jawaban A, B, C, D salah

Apabila bagian (b) diubah menjadi def := ghi(a,b) mod 10, maka berapakah hasil pemanggilan fungsi def(3,30)?
A. 1
B. 3
C. 7
D. 9
E. Jawaban A, B, C, D salah

function tebak_angka(x,y: integer): integer;
begin
  if x < 5 then begin
    case x of
      0: tebak_angka := 1;
      1: tebak_angka := 2;
      2: tebak_angka := 3;
      3: tebak_angka := 4;
      4: tebak_angka := 5;
    end;
  end else if x > y then begin
    tebak_angka := tebak_angka(y,x);
  end else begin
    tebak_angka := tebak_angka(x, y-(x mod 5)-1);
  end;
end;

Apakah outputnya jika perintah writeln(tebak_angka(18,30)) dipanggil?
A. 1
B. 2
C. 3
D. 4
E. 5