Olimpiade Sains Provinsi (OSP) 2010 - Komputer
Udin sudah bisa menjumlah bilangan, tetapi baru saja belajar menulis angka. Udin baru bisa menulis angka 1, 2, 3 dan 4. Tetapi dia tidak menyadari bahwa angka 1 dan 4 berbeda, bagi Udin “angka 4 adalah cara lain untuk menuliskan angka 1.” Selain itu bilangan beberapa dijit seperti 132 adalah bilangan yang bernilai sama dengan hasil penjumlahan dari digit-digit itu sendiri. Contoh : 132 = 1 + 3 + 2 = 6 dan 112314 = 1 + 1 + 2 + 3 + 1 + 1 = 9 (ingat, Udin menganggap 4 adalah 1). Sekarang, Udin ingin tahu berapa banyak cara yang dapat dilakukannya untuk menuliskan sebuah bilangan bernilai tertentu. Misalnya 2, Udin dapat menuliskan 5 bilangan yaitu : 11, 14, 41, 44 dan 2. Ada berapa banyak kemungkinan bilangan beberapa digit yang menurut Udin bernilai 3?
Panitia penyelenggara OSN bagian akomodasi mengatur penempatan para delegasi wakil-wakil provinsi di sebuah hotel. Delegasi-delegasi itu masing-masing dengan anggota yang jumlahnya bervariasi, dan rencana kedatangannya pun tidak bersamaan. Para anggota delegasi yang sama diasumsikan datang bersamaan. Karena jumlah kamar di hotel itu agak terbatas, panitia menetapkan suatu pengaturan. Selama kamar-kamar kosong masih tersedia, setiap kamar kosong ditempati oleh dua orang dari delegasi yang sama. Jika jumlahnya ganjil, yang satu orang itu akan ditentukan belakangan setelah yang berdua-berdua selesai ditempatkan. Selama masih ada kamar kosong, yang satu orang itu pun ditempatkan di kamar yang kosong. Saat tidak ada kamar kosong tesisa, setiap orang yang baru datang akan ditempatkan di kamar yang baru ditempati sendirian. Jika ada beberapa pilihan kamar kosong, selalu dipilih kamar dengan nomor yang paling kecil. Jika tidak ada lagi kamar kosong, tapi ada beberapa kamar yang masih satu orang, juga dipilih mulai dari kamar dengan nomor terkecil. Sekarang anda ketahui ada 8 kamar di hotel itu dan ada 8 delegasi yang akan datang yang jumlahnya berturut-turut sesuai dengan urutan waktu kedatangan adalah 3, 1, 3, 2, 1, 3, 2, 1. Jika kamar dinomori dari 1 sampai dengan 8, dan delegasi dinomori sesuai dengan urutan kedatangan dari 1 sampai 8, dengan siapakah anggota delegasi provinsi ke 8 akan sekamar?
Deskripsi untuk soal nomor 3 - 7
Terdapat N buah lampu b1, b2, …bn dan tombolnya masing-masing di bawah setiap lampu itu. Tombol itu berperilaku aneh, jika tombol suatu lampu bi ditekan sekali, lampu bi berubah dari mati menjadi terang atau dari terang menjadi mati. Selain itu, ada beberapa lampu yang ikut berubah, mati menjadi terang atau terang menjadi mati. Hubungan lampu-lampu lain yang ikut berubah dinyatakan dengan relasi (i, j). Jika relasi (i, j) itu ada, maka penekanan tombol di bi akan berdampak juga pada lampu di bj selain bi itu sendiri, dan sebaliknya, penekanan tombol di bj berdampak juga pada lampu di bi.
Ada 5 buah lampu: b1, b2, b3, b4 ,dan b5, dan terdapat relasi (1, 2), (1, 5), (2, 3), (2, 4), (3, 5), (4, 5). Jika mula-mula seluruh lampu mati, apa yang terjadi dengan b1 dan b2 jika dilakukan penekanan berturut-turut pada tombol-tombol b1, b2, dan b3, dan b5, masing-masing sekali? Jawab dengan memilih:
(A) keduanya mati,
(B) keduanya terang,
(C) b1 terang dan b2 mati, atau
(D) mati dan b2 terang
Jika mula-mula seluruh lampu mati, tuliskan berapa banyak penekanan sesedikit-sedikitnya untuk membuat semua lampu menjadi terang dilakukan?
Jika ditambahkan relasi (2, 4) dengan pertanyaan yang sama dengan no 4, bagaimana jawaban anda sekarang?
Seperti pada pertanyaan no. 5 yaitu adanya relasi tambahan (2, 4), kecuali hanya satu yang terang yaitu b2, tuliskan jumlah penekanan minimal (sesedikit mungkin) untuk membuat semua terang?
Untuk 8 lampu dengan relasi-relasi: (5, 8), (1, 5), (8, 6), (1, 2), (7, 3), ( 8, 3), (6, 7), (2, 6), (7, 5),(5, 4),(4, 2),(3, 4). Semula semua mati, berapa penekanan yang dilakukan sesedikitsedikitnya agar semua lampu menjadi terang?
Deskripsi untuk soal nomor 8 - 10
A dan B melakukan permainan batu. Terdapat N buah tumpukan batu. Di bagian bawah tumpukan terdapat kertas bertuliskan suatu bilangan bulat positif menyatakan nilai tumpukan. Setiap pemain bergantian mengambil satu batu. Setiap pemain yang mengambil batu terakhir dari suatu tumpukan akan mendapatkan skor sebesar nilai tumpukan ybs. Di awal permainan, jumlah batu setiap susunan diketahui, dan nilai-nilai tumpukannya juga diketahui.
Berikut ini ada 4 tumpukan seperti pada table di bawah ini. A hendak melakukan langkah pertama kalinya. Dengan asumsi B adalah pemain yang tidak pernah melakukan kesalahan dalam memilih langkahnya, hitunglah berapa skor akhir maksimum yang dapat ia kumpulkan.
| No Tumpukan | 1 | 2 | 3 | 4 |
| Nilai Tumpukan | 5 | 4 | 15 | 457 |
| Jumlah Batu pada tumpukan | 2 | 3 | 1 | 5 |
Berikut ini ada 8 tumpukan. A hendak melakukan langkah pertama kalinya. Dengan asumsi B adalah pemain yang tidak pernah melakukan kesalahan dalam memilih langkahnya, hitunglah berapa skor akhir maksimum yang dapat ia kumpulkan.
| No Tumpukan | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nilai Tumpukan | 5 | 4 | 15 | 457 | 345 | 13 | 235 | 346 |
| Jumlah Batu pada tumpukan | 2 | 3 | 1 | 4 | 5 | 1 | 3 | 2 |
Mengacu pada table di pertanyaan no. 0, seandainya aturan diubah: seorang pemain dapat mengambil 1 atau 2 batu pada setiap gilirannya dan A akan jalan pertama kali, siapakah yang akan mendapatkan nilai tumpukan ke empat?
Deskripsi untuk soal nomor 11 - 12
Suatu papan catur N x N setiapnya berisi bilangan nonnegatif. Di awal suatu bidak berada kotak (1, 1) atau yang di pojok kiri atas. Berikutnya secara berulang bidak dapat dipindahkan (1) horizontal ke kanan, atau (2) vertikal ke bawah sekian kotak sebanyak dengan bilangan pada kotak terakhir bidak itu berada, kecuali kalau membawa bidak keluar dari papan. Tujuan akhir adalah kotak (N, N) atau yang pojok kanan bawah. Bila bilangan terakhir adalah 0 dan bukan di pojok maka bidak berhenti (tidak dapat melanjutkan langkah kecuali kalau sudah mencapai tujuan).
Untuk papan catur berukuran 4x4 berikut ini temukanlah ada berapa lintasan langkah-langkah yang berbeda untuk membawa bidak dari posisi awal (kotak (1, 1)) ke tujuan (kotak (4,4)).
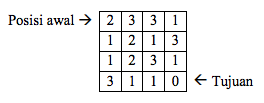
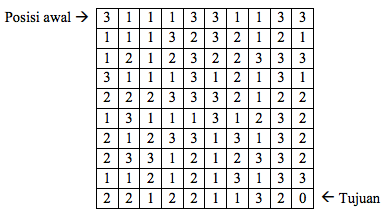
Untuk papan catur berukuran 4x4 berikut ini temukanlah ada berapa lintasan langkah-langkah yang berbeda untuk membawa bidak dari posisi awal (kotak (1, 1)) ke tujuan (kotak (10, 10)).
Deskripsi untuk soal nomor 13 - 15
Pak Umar menaruh barang berharganya di sebuah brankas (lemari besi) dengan kunci kombinasi 7 digit setiap digit adalah bilangan 0 sampai dengan 9.
Suatu ketika Pak Umar mengatur kombinasinya sedemikian rupa sehingga tidak ada digit yang digunakan berulang (setiap digit maksimum satu kali). Suatu ketika ia lupa bilangan kombinasi tersebut dan meminta anda untuk mencoba-coba berbagai kemungkinan. Ada berapa kemungkinan kombinasi yang mungkin anda harus coba?
Supaya tidak mudah kelupaan lagi ia men-set 3 digit berharga 0 (tidak tahu digit yang mana!) dan lainnya seperti sebelumnya maksimum hanya muncul 1 kali dalam kode (kecuali yang 0 tsb). Anda berancang-ancang kalau suatu ketika Pak Umar lupa kembali maka anda berhitung ada berapa kemungkinan kombinasi yang nanti harus dicoba.
Supaya semakin lebih mudah untuk diingatnya, maklum makin hari tambah pelupa saja, Pak Umar mensetnya kembali sedemikian rupa sehingga bilangan-bilangan itu tidak ada yang sama dan meningkat harganya dari kiri ke kanan. Ada berapa kemungkinan kombinasi?
Deskripsi untuk soal nomor 16 - 17
Dalam satu keluarga tedapat 8 bersaudara.kandung mereka adalah S, T, U V, W, X, Y dan Z. Urutan nama ini tidak berarti menunjukkan urutan umur, yang diketahui, orang-tua mereka melahirkan anak-anak itu dengan perbedaan hanya 1 tahun berturut-turut. Diketahui juga bahwa:
- Umur W lebih tua 4 tahun dari Z dan 3 tahun lebih muda dari X
- Sedangkan S lebih tua dari T, dan lebih muda dari X
- Umur U adalah umur rata-rata dari umur V dan X
Jika yang paling muda diketahui berumur 8, berapakah umur W ?
Jika V lebih muda dari W, manakah urutan yang paling mungkin dari pilihan di bawah ini jika diurutkan mulai dari yang tertua hingga yang termuda?
(A) X, S, U, W, V, T, Y, Z
(B) X, S, T, W, V, U, Y, Z
(C) Z, S, T, W, U, V, Y, X
(D) X, T, S, V, W, U, Z, Y
(E) X, U, S, T, W, V, Y, Z
Deskripsi untuk soal nomor 18 - 20
Dalam suatu acara jamuan makan malam yang diikuti oleh delapan orang (enam tamu ditambah tuan rumah dan nyonya rumah), mereka duduk di sekeliling meja memanjang. Para tamu, masing-masing tiga orang duduk di sisi-sisi meja. Tuan rumah duduk di salah satu ujung meja dan nyonya
Dari informasi di atas satu orang lagi yaitu Eko, periksalah apakah ia:
I. tuan rumah
II. duduk di sebelah kanan Diana
III. duduk di seberang Cindy
Berapa banyak dari ketiga pernyatan itu mana yang benar? (Jawab dengan menuliskan hanya angka-angka romawi dari pernyataan yang anda anggap benar, jika tidak ada yang benar jawab dengan “TIDAK ADA”).
Jika diketahui bahwa setiap orang duduk berseberangan dengan suami atau isterinya, mana di antara yang berikut ini yang pasti adalah pasangan suami isteri ?
(A) Gunawan dan Helena
(B) Brigitta dan Firman
(C) Cindy dan Firman
(D) Gunawan dan Brigitta
(E) Eko dan Helena
Di antara Ali, Brigitta, Cindy, Diana dan Eko, siapa dari mereka yang tidak duduk berdampingan dengan orang yang jenis kelaminnya sama dengannya?
Berikut ini ada dua potong algoritma pseupascal.
// pertama readln(x); repeat writeln(x); x := x + 1; Until x > 10;
//kedua readln(x); while x <= 10 do begin writeln(x); x := x + 1; end;
Apakah kedua potong algoritma itu berperilaku sama? Jika jawaban anda tidak, maka apa yang harus diharus dilakukan? Jawablah dengan memilih salah satu dari pilihan berikut dan menuliskan huruf pilihannya di lembar jawaban:
(A) sama, tidak perlu diapa-apakan lagi.
(B) tidak, pindahkan “readln(x)” ke dalam loop-while (sebelum “writeln(x)”).
(C) tidak, tambahkan “writeln(x)” setelah “readln(x)” dan sebelum loop-while.
(D) tidak, tambahkan “if x > 10 then writeln(x);” setelah “readln(x)”
(E) tidak, tambahkan “if x >= 10 then writeln(x);” setelah “readln(x)”
(F) ttidak, tapi tidak ada yang bisa dilakukan karena memang loop-repeat tidak bisa digantikan loop-while
Perhatikan potongan algoritma berikut.
for i := 1 to n do
for j := 1 to n do
XX(i,j);
Misalnya XX(i,j) dijalankan dengan harga berapapun bersifat konstan, dan potongan algoritma itu dengan harga n = 100, diperlukan waktu rata-rata 1 detik kira-kira berapa detik potongan algoritma ini dijalankan untuk nilai n = 2000?
Perhatikan potongan algoritma berikut.
i := 1;
while i <= n do
begin
j := 1;
while j <= n do
begin
writeln('*');
J := j * 10
end;
i := i * 2;
end;
Berapa kali karakter * dituliskan untuk n = 1000?
Mengacu pada potongan algoritma di pertanyaan no 23, jika n adalah suatu harga N yang cukup besar maka jumlah karakter * yang dituliskan proporsional dengan fungsi mana dari pilihan berikut ini?
(A) N
(B) N2
(C) log N
(D) N log N
(E)
(F) Tidak ada pilihan yang sesuai.
Perhatikan potongan algoritma berikut
funtion Z(l: integer; r: integer);
begin
if l < r then
z := z(l, ((l+r) div 2) - 1) + z(((l+r) div 2) + 1, r) + 1
else
z := 1;
end;
Berapakah yang akan dicetak pada pemanggilan fungsi Z(1, 10)?
Deskripsi untuk soal nomor 26 - 29
Tujuan dari algoritma ini adalah mencetak deret bilangan: 1, 2, 5, 10, 17, 26, 37, dan seterusnya selama hingga pertama kali mencetak angka yang > 1000.
i := 1; j := 1; while (i <= 1000) do begin writeln(i); ............ // perintah yang hilang j := j + 2; end; writeln(i);
Agar algoritma bekerja sesuai dengan yang diharapkan, perintah apakah yang harus dituliskan di bagian ............ // perintah yang hilang
Bila pada ekspresi pemeriksaan kondisi loop-while (perintah while (i <= 1000) do) variable i diganti dengan pemeriksaan variabel j menjadi while (j <= M) do berapakah harga yang terkecil yang mungkin untuk menggantikan M agar algoritma bekerja secara identik?
Bila angka 1000 pada ekspresi pemeriksaan kondisi loop-while (perintah while (i <= 1000) do) diganti dengan angka 10000, berapakah angka yang akan dicetak oleh perintah writeln(i) pada baris terakhir?
Bila angka yang terakhir dicetak diharapkan adalah angka terbesar yang lebih kecil dari 500, maka angka ke berapakah itu dalam deret yang dicetak (catatan: yang pertama adalah 1, kedua adalah 2, dst)?
Deskripsi untuk soal nomor 30 - 33
function hitung(a: integer): integer;
begin
if (a < 0) then
begin
write('-');
hitung(-a);
end
else if (a > 1) then
begin
tmp := hitung(a/2);
write(a mod 2)
end
else writeln(a);
end;
Apa yang akan dicetakkan pada pemanggilan hitung(100)?
Apa yang akan dicetakkan pada pemanggilan hitung(-150)?
Pada pemanggilan hitung(1000) berapa kali perintah write(a mod 2) akan dijalankan?
Untuk pemanggilan hitung(M) menghasilkan keluaran berupa bilangan berdigit 8 berapa bilangan terkecil M yang mungkin?
Deskripsi untuk soal nomor 34 - 37
var D:array[0..6] of char = ('A','B','C','D','E','F','G');
// procedure untuk menukarkan isi array D[a] dan D[b]
procedure swap(a: integer; b: integer);
var tmp: char;
begin
...... // perintah-perintah untuk menukarkan
end;
// procedure untuk mencetak isi array dalam satu baris.
procedure printarray;
var i: integer;
begin
........ // perintah-perintah untuk mencetak
end;
procedure ZZ(m: integer);
var i: integer;
begin
if (m <= 0) then
printarray
else
begin
ZZ(m-1);
for i := m-2 downto 0 do
begin
swap(i,m-1);
ZZ(m-1);
swap(i,m-1);
end;
end;
end;
Jika swap(a,b) dimaksudkan untuk menukarkan isi array D[a] dengan D[b], tuliskan perintahperintah yang seharusnya ada di bagian ". . . . . . . . ." di dalam procedure swap tersebut.
Pada pemanggilan ZZ(3), berapa kali procedure printarray akan dipanggil?
Misalkan ZZ(8) dijalankan di suatu computer selama 1 detik, kira-kira berapa lama ZZ(10) dijalankan?
Sebutkan SATU KATA saja yang menunjukkan proses apa yang dilakukan pseudocode ini pada data dalam array ?
Deskripsi untuk soal nomor 38 - 40
procedure cek(a: Boolean; b:Boolean; c: Boolean; d:Boolean);
begin
write(a,' ',b,' ',c,' ',d,' ');
if ((a and not b) or c ) and not ((c and b) or (d and not a)) then
writeln('kasus 1')
else
if ((not c and b) or (a and b and not c and d)) then
writeln('kasus 2')
else
if ((not a and not b and (c or d)) and (c and d)) then
writeln('kasus 3')
else writeln('kasus 4');
end;
Dengan suatu kombinasi harga a, b, c, d, prosedur mencetak "kasus 3", dengan kombinasi yang sama perintah writeln(a and b, ' - ',c and d) akan mencetak dua harga boolean apakah?
Dengan suatu kombinasi harga a, b, c, d, prosedur mencetak "kasus 1", dan diketahui a berharga true. dengan kombinasi yang sama perintah writeln(a and not b, , ' - ',not (c and d)) akan mencetak dua harga boolean apakah?
Bila (b and c) berharga true, maka keluaran yang dicetak adalah?