Sebuah bola pada ketinggian h dari permukaan lantai, ditembakkan secara horizontal dengan kecepatan v₀. Bola mengenai lantai dan memantul kembali. Proses tumbukan tersebut berlangsung elastik sebagian dengan koefisien restitusi e. Bola akan terus memantul berkali-kali sampai akhirnya tidak dapat memantul lagi.  Tentukan kapan (T) ini terjadi. Berapakah jarak horizontal L, yang ditempuh bola sampai keadaan ini?

Catatan : Percepatan gravitasi bumi adalah g. Anggap bola merupakan massa titik,  gesekan udara dan gesekan dengan lantai diabaikan.

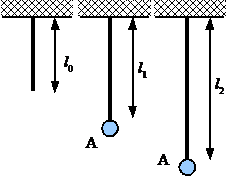
Sebuah karet ringan (massa dapat diabaikan) digantungkan pada langit-langit. Panjang karet dalam keadaan tidak tegang adalah l₀. Jika karet ditarik, maka karet dapat dianggap seperti pegas (yang memenuhi hukum Hooke). Karet tidak  memberikan gaya pulih  ketika panjangnya lebih kecil dari l₀.  Sebuah massa A digantung pada karet ini sehingga panjang karet (dalam keadaan setimbang) berubah menjadi l₁. Kemudian massa A ditarik ke bawah sampai panjang karet menjadi l₂. Berapakah panjang l₂ agar saat massa A dilepas (dari keadaan diam), dapat persis menyentuh langit-langit? Nyatakan jawaban anda dalam l₀ dan l₁.

Sebuah yoyo dengan massa m, jari-jari dalam r dan jari-jari luar R diletakkan di atas sebuah bidang miring dengan sudut kemiringan . Momen inersia yoyo terhadap pusat massanya adalah ½mR². Di ujung atas terdapat sebuah motor yang akan digunakan untuk menggulung benang dari yoyo.  Bidang miring licin dan posisi motor diatur sedemikan rupa sehingga benang sejajar dengan bidang miring (lihat gambar). Mula-mula semua sistem dijaga diam. Saat yoyo dilepas, motor mulai bekerja dengan kecepatan putar diatur sedemikian rupa sehingga pusat massa yoyo tidak mengalami perubahan posisi. Tentukan berapa besar daya motor sebagai fungsi waktu agar dapat memberikan keadaan ini.

Catatan : Anggap benang yang tergulung pada yoyo sangat panjang dan  abaikan massa benang. 

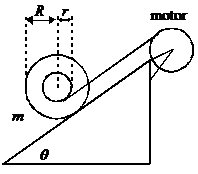
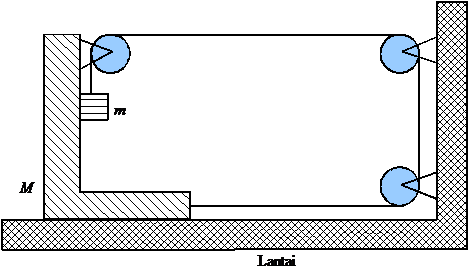
Perhatikan sistem seperti terlihat pada gambar di bawah. Sebuah massa M berbentuk huruf L dihubungkan pada massa m dengan tali yang melewati 3 buah katrol. Massa m persis menempel pada dinding massa M.  Mula-mula sistem diam. Tentukan vektor percepatan a_m saat massa m dilepas.

Catatan : Anggap massa M tidak bisa terguling dan tali tidak bisa mulur. Massa tali, massa katrol dan semua gesekan diabakan.

Sebuah bola m, berjari-jari R (I = 2/5 mR²) berada di atas sebuah bidang miring yang memiliki massa M. Ada gesekan  yang cukup besar antara bola dan bidang miring sehingga bola menggelinding turun tanpa slip. Berapakah koefisien gesek statis minimum µ_s antara bidang miring dan lantai agar bidang miring tidak bergerak sama sekali dalam proses ini?

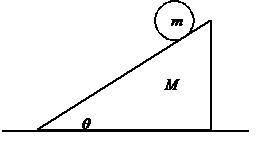
Sebuah massa titik m bergerak dengan kecepatan v₀ di atas lantai licin dan menabrak sebuah piringan (massa M = 3m  berjari-jari R). Tumbukan terjadi di titik A pada jarak h = 0,6 R dari garis horizontal yang melalui pusat piringan (lihat gambar).  Tentukan vektor kecepatan akhir (dalam arah x dan y)  kedua massa!

Catatan : Anggap tidak ada gesekan antara kedua massa dan tumbukan terjadi secara elastik.

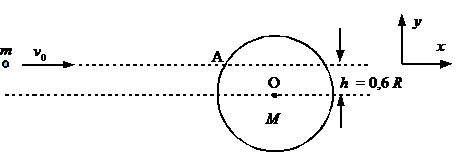
Perhatikan sistem seperti terlihat pada gambar. Bidang miring tidak dapat bergerak dan massa m₁ cukup besar sehingga dapat bergerak turun.

1. Tentukan percepatan massa m₁!
2. Berapakah batas minimum besar massa  m₁ agar dapat bergerak turun?

Catatan:  Massa tali dan katrol diabaikan dan tidak ada gesekan antara massa m₂ dengan bidang miring.