Olimpiade Sains Kota (OSK) 2018 - Matematika

Misalkan a,b dan c merupakan 3 bilangan berbeda. jika ketiga bilangan tersebut adalah bilangan asli 1 digit,maka jumlah terbesar akar-akar (x-a)(x-b)+(x-b)(x-c)=0 adalah.....

Setiap sel dari suatu tabel berukuran 2 × 2 dapat diisi dengan bilangan 1,2, atau 3. Misalkan N adalah banyaknya tabel yang memenuhi kedua sifat berikut sekaligus: 

• untuk setiap baris, hasil penjumlahannya genap

• untuk setiap kolom, hasil penjumlahannya genap

Nilai N adalah . . .

 Diberikan persegi berukuran 3 × 3 satuan seperti pada gambar. Luas segilima yang diarsir adalah ....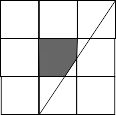

parabola y=ax²-4 dan y=8-bx² memotong  sumbu koordinat pada tepat empat titik. Keempat titik tersebut merupakan titik-titik sudut layang-layang dengan luas 24. nilai a+b adalah......

Untuk setiap bilangan asli n didefinisikan s(n) adalah hasil penjumlahan digit-digit dari n. banyanknya bilangan asli d sehingga d habis membagi n-s(n) untuk setiap bilangan asli n adalah....

diketahui x dan y adalah bilangan prima dengan x<y dan x³+y³+2018=30y²-300y+3018. nilai x adalah....

Diberikan dua bilangan asli dua angka yang selisihnya 10. Diketahui bahwa bilangan yang kecil merupakan kelipatan 3, sedangkan yang lainnya merupakan kelipatan 7. Diketahui pula bahwa jumlah semua faktor prima kedua bilangan tersebut adalah 17. Jumlah dua bilangan tersebut adalah . . .

 Diberikan satu koin yang tidak seimbang. Bila koin tersebut ditos satu kali, peluang muncul angka adalah  . Jika ditos n kali, peluang muncul tepat dua angka sama dengan peluang muncul tepat tiga angka. Nilai n adalah . . . 

 Panjang sisi-sisi dari segitiga merupakan bilangan asli yang berurutan. Diketahui bahwa garis berat dari segitiga tegak lurus dengan salah satu garis baginya. Keliling segitiga itu adalah . . .

Diberikan suku banyak p(x) dengan p(x)² + p (x² ) = 2x² untuk setiap bilangan real x. Jika   1 maka jumlah semua nilai p(10) yang mungkin adalah . . . 

Misalkan {x_n} adalah barisan bilangan bulat yang memenuhi x₁ = x₂ = · · · = x₁₂ = 0, x₁₃= 2, dan untuk setiap bilangan asli n berlaku

x_n+13 = x_n+4 + 2x_n.

Nilai x₁₄₃ adalah . . .

. Untuk setiap bilangan real z,  menyatakan bilangan bulat terbesar yang lebih kecil dari atau sama dengan z. Jika diketahui dan . Nilai 10(x + y) adalah . . . 

Misalkan ABCD adalah trapesium siku-siku dengan AB sejajar DC dan AB tegak lurus AD. Misalkan juga P adalah titik potong diagonal AC dan BD. Jika perbandingan luas segitiga AP D dan luas trapesium ABCD adalah 4 : 25 maka nilai adalah . . . 

Himpunan S merupakan himpunan bilangan-bilangan 7 digit sehingga masing-masing angka 1, 2, 3, 4, 5, 6, atau 7 tepat muncul satu kali. Bilangan-bilangan di S diurutkan mulai dari yang paling kecil sampai yang paling besar. Bilangan yang berada pada urutan ke-2018 adalah . . . 

misalkan S={}. banyaknya pasangan bilangan asli (a,b) yang dapat sehigga tepat ada 2018 anggota S yang dapat dinyatakan dalam bentuk  untuk suatu bilangan bilat x dan y adalah....

Diberikan segitiga ABC dan lingkaran R yang berdiameter di AB. lingkaran R memotong sisi AB dan BC berturut-turut di D dan E. Jika ,maka luas segitiga ABC adalah.......

diberikan bilangan real x dan y sehingga memenuhi 

 nilai minimum dari  adalah......

diberikan sembilan titik seperti pada gambar.pada tiap sisi,dua titik yang bukan titik sudut segitiga membagi sisi menjadi tiga bagian

sama panjang.kesembilan titik ini akan diwarnai dengan warna merah atau biru. peluang bahwa dari kesembilan titik tersebut 

terdapat tiga titik yang warnanya sama dan membentuk segitiga siku-siku adalah.......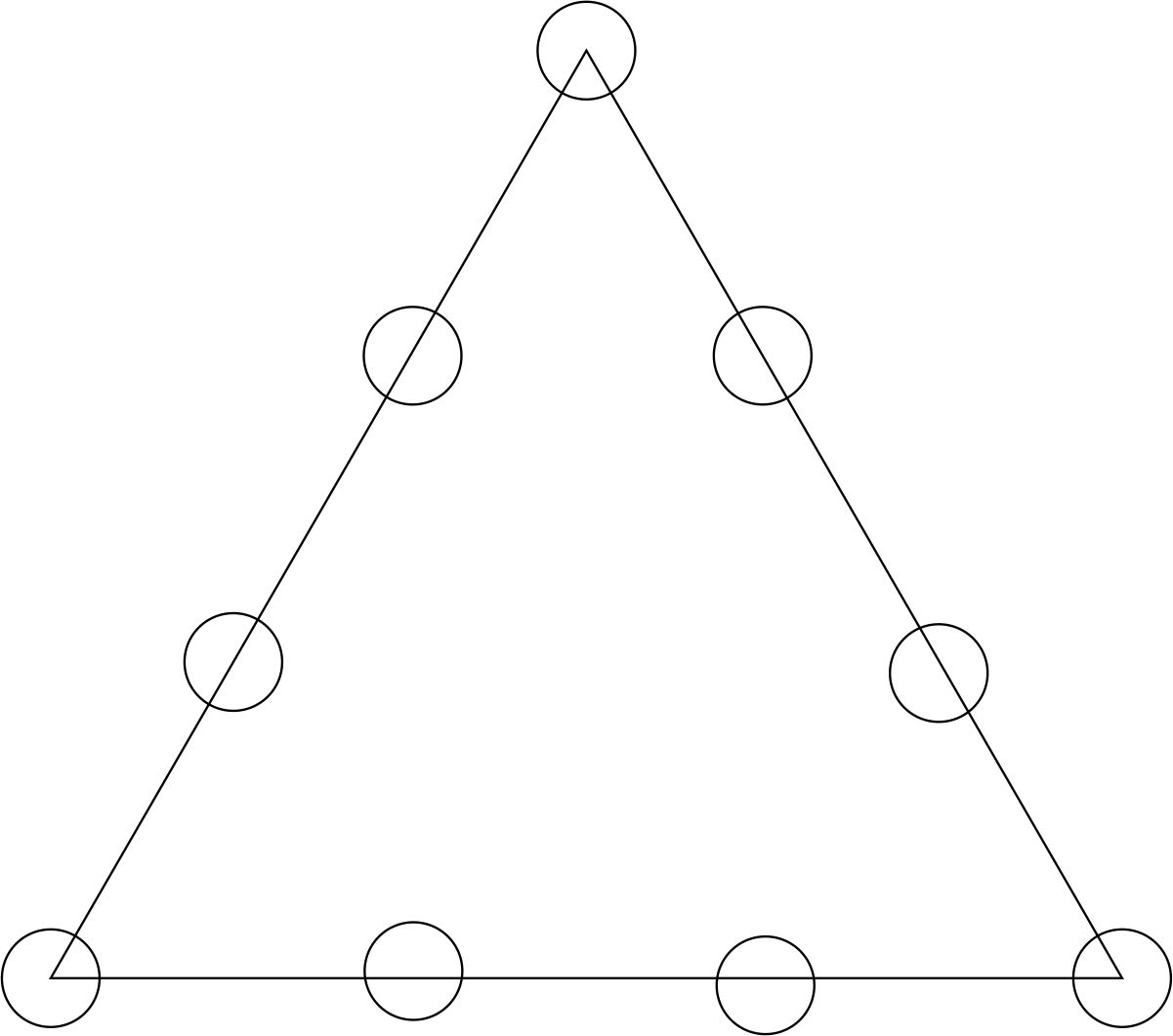

 

19. Bilangan prima terbesar yang dapat dinyatakan dalam bentuk a⁴ + b⁴+ 13 untuk suatu bilangan-bilangan prima a dan b adalah . . . 

Pada segitiga ABC, panjang sisi BC adalah 1 satuan. Ada tepat satu titik D pada sisi BC yang memenuhi |DA|² = |DB| · |DC|. Jika k menyatakan keliling ABC, jumlah semua k yang mungkin adalah . . .