Olimpiade Sains Kota (OSK) 2011 - Komputer
11100 mod 41 =
a. 1
b. 19
c. 20
d. 29
e. 40
11 x 22 x 33 x 44 x 55 x ... x 3030 dapat habis dibagi oleh 10n. Berapakah bilangan n terbesar yang mungkin?
a. 105
b. 130
c. 30
d. 150
e. 110
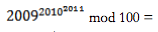
a. 1
b. 9
c. 21
d. 69
e. 81
Bilangan 6075 habis dibagi bilangan-bilangan positif: n1, n2,.. n3 dst. Jika bilangan-bilangan tersebut dijumlahkan adalah ...
a. 11281
b. 11282
c. 11283
d. 11284
e. 11285
A sedang berada di taman di posisi titik yang disilang dan ingin menghitung jumlah pohon yang terlihat. Pohon ditanam dengan jarak antar 2 pohon yang bersebelahan 1 meter, dan diletakkan pada tiap titik. Pada taman yang berukuran 3x3 meter seperti gambar dibawah, terdapat total 15 pohon, berapakah pohon yang bisa dilihat oleh A? A tidak bisa melihat pohon yang tepat berada di belakang pohon lain dengan jalur penglihatan yang sama.
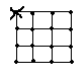
a. 3
b. 9
c. 10
d. 12
e. 15
Deskripsi untuk soal nomor 6 - 7
A,B,C,D,E,F,G,H sedang ingin menonton bioskop. Karena penontonnya sudah banyak, posisi duduk yang mereka dapat seperti gambar ini.
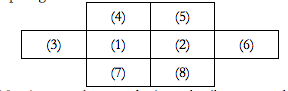
Manajer yang akan memberi mereka tiket mengetahui beberapa hal berikut:
-
Tiap orang tidak ingin duduk berdekatan dengan orang yang mereka benci
-
A dan B saling membenci
-
G dan H saling membenci
-
C membenci B dan D
-
F membenci E dan G
- D membenci E
Siapa yang akan duduk ditengah-tengah (1), (2)?
a. B dan G
b. E dan G
c. A dan H
d. D dan F
e. C dan E
Siapa yang akan duduk dibagian paling pinggir (3), (6)?
a. A dan H
b. D dan F
c. E dan G
d. B dan G
e. C dan E
Deskripsi untuk soal nomor 8 - 9
Seorang salesman (petugas pemasaran) suatu perusahaan minuman harus mengunjungi 5 warung untuk memperkenalkan produk minuman terbaru. Kelima warung tersebut adalah: P, Q, R, S, dan T. Dia hanya akan mengunjungi masing-masing satu kali saja, satu warung per hari, Senin s/d Jumat, dengan aturan berikut:
-
Tidak boleh mengunjungi warung R pada hari Senin.
-
Harus mengunjungi warung P sebelum mengunjungi S.
- Harus mengunjungi warung Q sebelum mengunjungi T.
Mana jadwal yang memenuhi syarat?
a. Q, S, P, T, R
b. R, Q, T, P, S
c. R, S, P, Q, T
d. T, R, Q, P, S
e. P, S, R, Q, T
Jika ia mengunjungi R lebih dahulu daripada P, mana yang pasti benar?
a. Q dikunjungi pertama kali
b. R dikunjungi pada hari Selasa
c. P dikunjungi pada hari Rabu
d. T dikunjungi pada hari Kamis
e. S dikunjungi terakhir kali
Deskripsi untuk soal nomor 10 - 11
Kali ini kita akan menyelidiki permainan tradisional lempar bom sembunyi tangan. Permainan ini dimainkan oleh beberapa pemain yang membentuk lingkaran. Permainan ini dimulai dengan memberikan salah satu orang tersebut sebuah bom mainan. Bom mainan tersebut memiliki suatu angka positif. Apabila angka tersebut menjadi 0 saat dipegang salah satu pemain, maka bom tersebut akan meledak dan pemain yang saat itu sedang memegang bom tersebut dinyatakan gugur. Setiap pemain saat baru mendapatkan bom (baik saat awal permainan maupun saat diberikan temannya seperti dijelaskan di bawah) harus mengurangi angka di dalam bom tersebut dengan 1. Setelah itu, bom tersebut diberikan pada temannya yang ada di arah sesuai jarum jam. Untuk mempermudah representasinya, kita akan beri nomor pemainnya dimulai dari 1 untuk pemain yang pertama kali mendapatkan bom, 2 untuk pemain yang ada tepat di sebelahnya searah jarum jam, 3 untuk yang setelahnya di arah jarum jam dan terus sampai seluruh pemain mendapatkan nomor.
Apabila bom tersebut pada awalnya memiliki angka 825, maka apabila permainan dimainkan oleh 5 pemain maka pemain berapakah yang akan gugur?
a. 1
b. 5
c. 4
d. 2
e. 3
Apabila permainan dimainkan oleh 5 pemain, angka manakah yang apabila menjadi angka mulai bom tersebut akan membuat pemain nomor 3 gugur?
a. 5573
b. 2749
c. 9090
d. 1322
e. Tidak ada jawaban yang benar atau ada lebih dari 1 jawaban yang benar
Deskripsi untuk soal nomor 12 - 14
Di suatu negara, ada 6 kota (a,b,c,d,e,f) dan 3 jalur kereta api, K1, K2, dan K3. Karena keterbatasan jumlah kereta api, setiap kereta api hanya mempunyai jadwal keberangkatan sebagai berikut :
-
Kereta K1 berangkat pukul 9.10 dan pukul 15.40 dengan jalur e-a-b-d
-
Kereta K2 berangkat pukul 7.00 dan pukul 16.50 dengan jalur f-c-e-b
- Kereta K3 berangkat pukul 12.25 dan pukul 15.40 dengan jalur d-a-f-e
Setiap kereta membutuhkan waktu 1 jam untuk berpindah dari 1 kota ke kota lain dan berhenti di suatu stasiun selama 5 menit lalu lanjut ke kota selanjutnya. Biaya naik kereta selalu sama setiap saat untuk setiap kereta (tidak peduli hari raya dan kenaikan harga cabe).
Jika seseorang sudah siap berangkat dari kota a pada pukul 9.00, pada jam berapa paling cepat dia sampai di kota e jika menggunakan kereta api?
a. pukul 15.30
b. pukul 15.35
c. pukul 15.40
d. pukul 17.50
e. pukul 17.55
Jika seseorang berada di kota a pada pukul 13.00, pada pukul berapa dia paling cepat sampai di kota c?
a. pukul 15.35
b. pukul 16.45
c. pukul 16.40
d. pukul 17.50
e. pukul 17.45
Jika seseorang berangkat dari kota e dan ingin menuju ke kota f (tanpa turun dari kereta), lalu menuju ke kota b (tanpa turun dari kereta), lalu kembali ke kota e: berapa kali minimal perpindahan kereta yang dilakukan agar biaya tiket seminimal mungkin ?
a. 6 kali
b. 3 kali
c. 2 kali
d. 4 kali
e. 5 kali
Didefinisikan N! = N x (N-1) x.. x 2 x 1 dan N# = N + (N-1) + ... + 2 +1
Contoh :
4! = 4 x 3 x 2 x 1 = 24
4# = 4+3+2+1 = 10
Berapa digit terakhir dari ((5#)#) + ((3#)#) - ((5!)! + (3!)!) ?
a. 4
b. 3
c. 2
d. 1
e. 0
Pak Dengklek ingin memasang ubin pada lantai berukuran 3 x 10 m2. Ubin yang dimiliki oleh Pak Dengklek berukuran 3 x 1 m2. Berapakah banyaknya cara penyusunan yang bisa dipakai oleh Pak Dengklek untuk menyusun ubin tersebut?
a. 13
b. 21
c. 19
d. 23
e. 28
Pada sebuah kantong terdapat 2 buah kelereng kuning, 5 buah kelereng biru, dan 8 buah kelereng hitam. Berapa minimal banyaknya kelereng yang perlu diambil agar kita pasti mendapatkan setidaknya 5 kelereng bewarna sama?
a. 10
b. 11
c. 9
d. 13
e. 12
Pada toko kue Pak Dengklek dijual 12 jenis kue. Ali ingin membeli 4 buah kue di toko kue tsb. Setiap jenis kue tersedia setidaknya 4 buah. Berapa banyak kombinasi jenis kue yang bisa dibeli Ali termasuk kemungkinan bahwa dari 4 kue tsb. ada yang jenisnya sama?
a. 370
b. 1365
c. 11880
d. 564
e. 495
Pada tanggal 4 Januari tahun ini, Anisa datang ke pasar. Dua hari kemudian, Budi juga datang ke pasar itu. Jika Anisa datang ke pasar setiap 11 hari sekali dan Budi datang setiap 7 hari sekali, kapan mereka bertiga bertemu di pasar? (asumsikan 1 bulan itu 30 hari)
a. 17 Januari tahun ini
b. 25 Januari tahun ini
c. 17 Februari tahun ini
d. 17 Maret tahun ini
e. 25 April tahun ini
Suatu gedung dikerjakan oleh 20 orang pekerja. Pekerjaan itu akan selesai dalam 100 hari. Namun, setelah 40 hari bekerja, 5 orang pekerja mengalami kecelakaan sehingga para pekerja berkabung selama 1 hari(tidak bekerja). Hari selanjutnya, mereka melanjutkan pekerjaan tersebut. Namun, karena masih berada dalam suasana berkabung, ada 10 orang pekerja yang kecepatan bekerjanya berkurang 20% dan sisanya mengundurkan diri. Berapa total waktu yang dibutuhkan untuk menyelesaikan pekerjaan tersebut dimulai dari hari pertama kerja?
a. 185
b. 184
c. 190
d. 191
e. 161
Berapa banyak angka antara 100 hingga 1000 yang habis dibagi 3 dan 5 tetapi tidak habis dibagi 30?
a. 48
b. 40
c. 30
d. 20
e. 18
1/2 + 1/6 + 1/12 + 1/20 + ... + 1/9900 =
a. 99/100
b. 96/100
c. 98/100
d. 97/100
e. 100/100
Deskripsi untuk soal nomor 23 - 24
Pada suatu ruangan, terdapat beragam binatang berkaki empat dan beragam binatang berkaki dua. Jumlah seluruh binatang adalah 112 ekor. Jumlah seluruh kaki binatang-binatang tersebut adalah 310.
Berapa ekorkah binatang yang berkaki dua?
a. 86
b. 43
c. 69
d. 37
e. 75
Berapa ekorkah binatang yang berkaki empat?
a. 37
b. 69
c. 75
d. 43
e. 86
Diberikan enam pulau yang saling terisolasi yang dilambangkan sebagai lingkaran. Garis putus-putus melambangkan jembatan yang dapat dibangun antara pulau-pulau. Angka di dekat garis putus-putus melambangkan biaya untuk membangun jembatan tersebut.
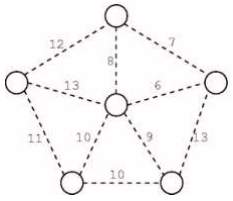
Berapakan minimal jumlah jembatan yang harus dibangun untuk menghubungkan enam pulau tersebut sehingga paling sedikit ada satu rute yang untuk mengunjungi antara setiap pasang pulau?
a. 9
b. 5
c. 7
d. 6
e. 8
Sebuah lingkaran akan dibagi-bagi menjadi sejumlah bidang yang dibentuk dengan menggambar garis lurus yang memotong dua tepi lingkaran. Dengan menggambar 3 garis sebagai berikut, terbentuk 4 atau 5 bidang

Berapa bidang maksimal yang dihasilkan dengan 3 garis?
a. 9
b. 5
c. 7
d. 6
e. 8
Pak Birla beserta istri dan Pak Tata beserta istri bertanding pada turnamen catur (sistem gugur). Dari 3 pertandingan yang dimainkan:
1) Hanya pada pertandingan pertama, suami dan istri bertanding
2) Laki-laki memenangkan 2 pertandingan dan perempuan memenangkan hanya 1 pertandingan
3) Keluarga Birla memenangkan pertandingan lebih banyak daripada keluarga Tata
4) Siapa yang kalah tidak bisa bermain untuk pertandingan selanjutnya
Siapa yang tidak pernah kalah?
a. Bu Tata
b. Pak Tata
c. Bu Birla
d. Pak Birla
e. Tidak ada jawaban yang benar
Sebuah password (kata sandi) yang terdiri dari 5 angka. Angka ke-4 lebih besar daripada angka ke-2 dengan selisih 4. Sementara angka ke-3 kurang dari angka ke-2 dengan selisih 3. Angka pertama adalah 3 kali lipat angka terakhir. Ada 3 pasang angka dengan jumlah 11. Berapakah angka ke-4 dari password tersebut?
a. 9
b. 5
c. 7
d. 3
e. 4
Ada dua orang yang berdiri pada sebuah jalan. Seseorang berkata pada yang lain, "Aku punya 3 anak, hasil perkalian umur mereka ada 36. Berapa umur anak PALING TUA?"
Orang kedua berkata, "Aku BELUM BISA menentukan. Aku butuh informasi tambahan." Orang pertama kemudian berkata "Jumlah umur mereka sama dengan nomor rumah paling ujung di jalan ini yang dapat kita lihat dengan jelas"
Orang kedua berkata lagi, "Aku MASIH BELUM BISA menentukan. Aku butuh informasi tambahan." Orang pertama kemudian berkata "Semua Anak sudah berusia lebih dari satu tahun "
Orang kedua berkata lagi, "Aku sudah bisa menentukannya"
Berapa umur anak PALING TUA?
a. 4
b. 6
c. 9
d. 12
e. 18
Joko sering berbohong (jangan ditiru). Dia hanya jujur sehari dalam seminggu. Satu hari dia berkata: "Aku berbohong pada Senin dan Selasa". Pada hari selanjutnya dia berkata: "Hari ini adalah salah satu dari hari Minggu, Sabtu atau Kamis". Pada hari selanjutnya dia berkata: "Aku berbohong pada Jum'at dan Rabu". Pada hari apa dia berkata jujur?
a. Senin
b. Selasa
c. Kamis
d. Jum'at
e. Minggu
Ada berapa banyak bilangan di antara 10 sampai dengan 100 yang habis dibagi 3?
a. 9
b. 10
c. 12
d. 30
e. 90
Deskripsi untuk soal nomor 32 - 34
Enam (6) orang diurutkan dari 1-6 menurut tinggi badannya (Urutan pertama paling pendek, urutan ke-6 paling tinggi) dan dari 1-6 menurut berat badannya. (Urutan pertama paling ringan, urutan ke-6 paling berat). Nilai tiap orang adalah hasil jumlah kedua nilai urutan tersebut. Hasil perhitungan menyatakan bahwa :
-
Gayun lebih tinggi dari Mila dan lebih ringan dari Budi
-
Heni lebih tinggi dari Gayun dan lebih ringan dari Ayin
-
Cici lebih pendek dari dan lebih berat dari Gayun
- Mila lebih tinggi dari Ayin dan lebih berat dari Cici
Siapakah di antara mereka yang dapat dipastikan lebih tinggi dan sekaligus lebih ringan dari Cici.
a. Ayin
b. Budi
c. Gayun
d. Heni
e. Mila
Berapa banyak orang yang mungkin lebih berat dan sekaligus lebih tinggi dari Gayun?
a. 0
b. 1
c. 2
d. 3
e. 4
Jika semua Aps adalah Eps, semua Eps adalah Ops, dan semua Ops adalah Ups, maka manakah yang tidak benar?
a. Semua Eps adalah Ups
b. Semua Aps adalah Aps
c. Semua Aps adalah Ops
d. Semua Aps adalah Ups
e. Semua Ops adalah Aps
Perhatikan gambar persegi ajaib berukuran 4x4 di bawah ini:
| 4 | ? | 5 | X |
| 14 | Z | 11 | ? |
| ? | 6 | Y | 3 |
| 1 | ? | 8 | 13 |
Jika persegi ajaib tersebut diisi bilangan bulat dari 1 sampai dengan 16 sedemikian rupa sehingga total bilanganbilangan dalam setiap kolom/baris/diagonal adalah sama, maka X + Y + Z = ...
a. 34
b. 33
c. 32
d. 31
e. 30
Perhatikan potongan program berikut
ayam := 100;
bebek := 5;
repeat
bebek := bebek +1 ;
ayam := ayam - bebek;
until ayam > bebek ;
writeln (ayam, ‘ dan ’, bebek);Manakah pasangan nilai (ayam,bebek) yang akan dicetak?
a. 94 dan 6
b. 100 dan 5
c. 10 dan 14
d. salah semua
e. program tak berhenti
Perhatikan Program sebagai berikut
input(n);
j:=n-1;
for i:=j downto 2 do
begin
n:=i mod n;
end;
writeln(n);berapakah outputnya jika diinputkan n = 97
a. 96
b. 0
c. 1
d. 2
e. 3
Perhatikan potongan program berikut
begin
readln(n);
i:=0;
while i<n do
begin
i:=i+4;
if (i<n) then
for j:=1 to 4 do
write('*');
end;
end;Berapa kali '*' ditulis dilayar jika input n adalah 20?
a. 24
b. 8
c. 12
d. 16
e. 30
Perhatikan potongan program berikut:
function adadeh(n : longint);
var i,j,k : longint;
begin
adadeh:=0;
for i:=1 to n do
for j:=1 to n+1 do
for k:=1 to n+2 do
adadeh:=adadeh+1;
adadeh:=adadeh div 6;
end;Berapakah nilai n minimal agar adadeh(n) lebih dari 200?
a. 12
b. 10
c. 4
d. 5
e. 6
Perhatikan potongan program berikut
function a(n:integer):integer;
begin
if (n=0) then
a:= 0;
else
a:= 1-n*a(n-1);
end;Berapakah hasil dari a(5)?
a. -120
b. -76
c. 120
d. 0
e. 76
Perhatikan urutan operasi-operasi terhadap 3 variabel Boolean a,b, dan c pada program sebagai berikut :
a := a XOR b;
b := a AND b;
a := a XOR b;
b := a AND b;
c := a XOR b;Manakah dari ekspresi berikut yang bernilai sama dengan nilai c di baris terakhir program ?
a. NOT b
b. a AND (NOT b)
c. a XOR b
d. a AND b
e. Tidak ada jawaban yang benar
Perhatikan prosedur berikut ini.
procedure TOKI(k:integer);
begin
if (k >1) then
begin
if k mod 2 =0 then
TOKI(k div 2)
else
TOKI(3*k+1);
if k mod 5 =1 then
write('T');
if k mod 5 =2 then
write('O');
if k mod 5 =3 then
write('K');
if k mod 5 =4 then
write('I');
end;
end;
Berapa banyak huruf 'K' yang tertulis bila dipanggil
TOKI(20)?
a. 5
b. 4
c. 3
d. 2
e. 1Jika array a berisi (-3, 8, 17, -10, 7, -5, -9, 2, 8, 1), apa output yang dihasilkan jika potongan program tersebut dieksekusi?
a. 17
b. 21
c. 25
d. 39
e. 31
Jika array a berisi (8, 3, 5, 21, x, 6, 10, 4), berapakah nilai x yang menghasilkan output maksimal jika potongan program tersebut dieksekusi?
a. 13
b. 10
c. 9
d. 0
e. -12
Perhatikan prosedur sebagai berikut
procedure esrever(var i,j:integer);
var k:integer;
begin
k:=i;
i:=j;
j:=k;
writeln(j,' ',i);
end;Apa output di layar jika dipanggil dengan parameter esrever(2,100)?
a. 2 2
b. 100 2
c. 2 100
d. 100 100
e. Tidak ada jawaban yang benar
Diberikan penggalan program sebagai berikut. (note: program ini merupakan Pascal-like pseudocode, secara sintaks belum tentu sama dengan Pascal)
function f (n: integer);
begin
if n=0 then f:=0
else f := n + f(n-1);
end;Untuk f(8) program di atas menghitung:
a. 0+1+2+3+4+5+6+7+8
b. 1+2+3+4+5+6+7+8
c. 8+7+6+5+4+3+2+1
d. 8+7+6+5+4+3+2+1+0
e. Tidak ada jawaban benar
Perhatikan potongan program berikut
for i := 1 to n do begin
for j := 1 to n do begin
for k := 1 to n do begin
writeln('Hello');
end;
end;
end;Dengan sembarang harga n > 0, keluaran 'Hello' akan dicetak berulang-ulang dalam sejumlah baris yang
a. merupakan konstanta
b. merupakan fungsi kuadrat dari n
c. merupakan fungsi linier dari n
d. merupakan fungsi pangkat empat dari n
e. merupakan fungsi kubik (pangkat 3) dari n
Perhatikan potongan program berikut
if x > y then
if z > x then
t := z;
else t := x;
else
if z > y then
t := z;
else t := y;
writeln(t);Apabila diberikan nilai x=3, y=5 dan z=8, berapakah output dari program tersebut?
a. 7
b. 8
c. 3
d. 5
e. 4
Perhatikan potongan program berikut
Data := Init;
x := 0;
for i := 0 to Data-1 do
begin
x := x + 2*i;
end;
writeln(x);Berapakah nilai Init sehingga program di atas menghasilkan output x tertulis 90 ?
a. 9
b. 45
c. 11
d. 10
e. 0
Perhatikan tahapan-tahapan berikut: Misalkan ada dua variable "x" dan "y", dan variable "hasil" yang nilai awalnya 0. Lakukan proses berikut selama nilai "x" lebih besar dari 0:
-
Jika nilai "x" ganjil maka nilai "hasil" := "hasil" + y.
-
nilai "x" selanjutnya adalah nilai "x" sebelumnya dibagi dua, bila ada hasil pecahan, maka pecahannya di buang. (contoh bila nilai "x" sebelumnya 1, maka nilai "x" selanjutnya 0)
- nilai "y" selanjutnya adalah nilai "y" sebelumnya dikali dua
Manakah program pseudo-pascal yang merupakan program dari tahapan-tahapan tersebut? (catatan: fungsi "mod" memberikan nilai sisa bagi, contoh: 13 mod 5 = 3 dan fungsi “div” membagi dan membulatkan ke bawah)
a.
var x,y : integer
x := 10;
y := 15;
hasil := 0;
while x > 0
begin
if (y mod 2 = 1) then begin hasil := hasil + y; end;
x := x * 2;
y := y div 2;
endb.
var x,y : integer
x := 10;
y := 15;
hasil := 0;
while x > 0
begin
if (x mod 2 = 1) then begin hasil := hasil + y; end;
x := x div 2;
y := y * 2;
endc.
var x,y : integer
x := 10;
y := 15;
hasil := 0;
while x > 0
begin
if (x mod 2 = 1) then begin hasil := hasil + x; end;
x := x * 2;
y := y div 2;
endd.
var x,y : integer
x := 10;
y := 15;
hasil := 0;
while x > 0
begin
if (x mod 2 = 1) then begin hasil := hasil + x; end;
x := x div 2;
y := y * 2;
ende.
var x,y : integer
x := 10;
y := 15;
hasil := 0;
while x > 0
begin
if (y mod 2 = 1) then begin hasil := hasil + y; end;
x := x div 2;
y := y * 2;
end